Dave Computes
Sunday, November 5, 2023
Dave Computes Fibonacci Paths
Monday, July 31, 2023
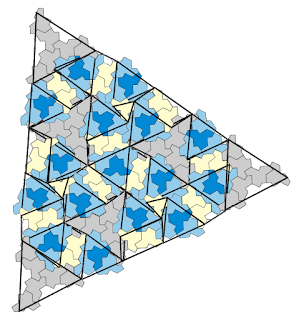
Dave Computes Fibonacci Triangles (joined at edges)
This is the third post in a series that began with my post on Fibonacci Bands in Aperiodic Patterns. The second post in the series focused on patterns created by joining Fibonacci triangles at their vertices. In this post, we'll look at related aperiodic patterns created by joining Fibonacci triangles at their edges. As before, we start with an equilateral triangle whose side lengths correspond to a Fibonacci number. In this case, I've started with a 13-triangle.
Saturday, July 29, 2023
Dave Computes Fibonacci Triangles (joined at vertices)
This is a continuation of my post on Fibonacci Bands in Aperiodic Patterns. This time we'll look at using these bands to generate patterns with threefold rotational symmetry. The image on the left shows a set of horizontal Fibonacci bands. A second set of bands has been added to the figure on the right, rotated 120 degrees.
And a third set of Fibonacci bands has been added to the image below, rotated another 120 degrees.
In the image above, 48.8% of the pixels are colored yellow. These correspond to places where a single 0-band crosses a pair of 1-bands. Here's a breakdown of the pixels in the image.
3 0 blue 7.3%
2 1 green 22.1%
1 2 yellow 48.8%
0 3 red 21.7%
Here is the same image, colored black only where three 0-bands meet (the blues in the original image).
Notice the triangles are all the same size, and they appear in two different orientations. Together, they form an isometric grid without any gaps. This only occurs when the Fibonacci bars are tuned just right. The animation below shows that when the horizontal bars are shifted upward, different sized shapes appear and disappear, often leaving gaps.
Here is that same image again, this time colored black wherever two or three 0-bands meet (the blues and greens in the original image).
In the animation below, the black pixels occur where three 0-bands or three 1-bands meet (reds and blues in the original image).
There are some really interesting moments in this animation, like the ones shown below (colored to highlight shapes). Each one seems like a set of tiles with its own rules.