Dave Computes Multiplication With Rulers

In this post, we're going to see how to multiply with rulers. Along the way, we'll learn how slide rules work and how to make your own, along with a bit about logarithms.


Part 1:  Adding With Rulers

To start, let's see how to add with 10-inch rulers.

We'll use two such rulers, one on top of the other. Place them so the left edge of the top ruler lines up with the 2 on the bottom ruler:

Notice that the values on the bottom ruler are now 2 more than the values in the corresponding positions of the top ruler. We can therefore now compute 2 + 3 by finding the 3 on the top ruler and then finding the sum (5) just below it on the bottom ruler. In general, to find x + y, place the left edge of the top ruler at x on the bottom ruler, find y on the top ruler, and the sum x + y will be just below it on the bottom ruler.

We can subtract, too. Let's say we want to find 7 - 4. We think of this as "4 plus what gives us 7" Line the rulers up so that the left edge of the top ruler is at the 4 on the bottom ruler. Find the sum (7) on the bottom ruler, and the answer (3) appears above it.

Let's try a trickier problem. If we attempt to find 7 + 5 in this manner, something goes wrong. The sum should be below the 5 on the top ruler, but we've run out of ruler!

We could solve this problem by introducing a third ruler, but we don't have to. Instead, we'll line up the right edge of the top ruler with the 7 on the bottom ruler. We look for the number below the 5, and find 2 there. This represents the ones digit of the sum. Essentially, by placing the right side of the top ruler at 7, we've computed 7 - 10 + 5 = 2. We just need to add 10 to our final answer to see that 7 + 5 = 12.

One more thing to note. When we line up the left edges of the rulers, the top and bottom numbers match. We can think of this as adding 0. Thus, the left edge of the ruler must be 0--the identity element for addition.

Part 2:  Multiplying with Rulers

Surprisingly, it turns out we can also multiply with rulers, but we'll need to mark them differently. Beginning from an unmarked ruler, we first need to make a single arbitrary decision. What number should we put on the right edge? When adding, the right side represented 10, and that made adding a bit easier in our base-10 system (see 7 + 5). So let's also put 10 on the right edge of our multiplication rulers.

For addition, the choice to put 10 on the right side of the ruler fixes the locations of any other numbers we wished to mark. The same is true for multiplication. Let's line up two multiplication rulers.

This picture represents a multiplication problem:  something times 10 equals 10. Clearly, that something must be 1, the identity element for multiplication. So, for multiplication rulers, the left edge represents the value 1 (not zero).

But how can we locate numbers between 1 and 10? Let's figure out where the number 2 belongs.

If we line up 3 rulers end to end, the values on the rulers will span from 1 to 1,000.

By a lucky coincidence, 2¹⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1,024 is very close to 1,000. That means that we can multiply by 2 ten times in roughly the span of three rulers.

Divide 3 rulers by 10 to find that we can multiply by 2 once in roughly 0.3 rulers (0.301 would be more exact). On a 10-inch ruler, we would therefore write the number 2 at the 3" mark.

We can now go about finding other numbers on our ruler. Using two rulers, we can compute 2 × 2 and write the result (4) at the corresponding position (near the 6" mark of a 10" ruler).

Now we compute 2 × 4 and write that result (8) there (near the 9" mark).

Notice that we've basically turned multiplication into addition. Adding the lengths of rulers is telling us the results of multiplication problems. We can also perform division with our rulers. Consider the question "2 times what equals 10?" This lets us find where to write the number 5 (near the 7" mark).

Using nothing but multiplication and division by 2, we could go on to find decimal values. For example, we could ask "2 times what equals 5" to find 2.5 (near the 4" mark).

Alternatively, we could compute 2 × 8 to find 16.

Unfortunately, we've run out of ruler, so instead we'll position the right edge of the top ruler on the 2 from the bottom ruler. This has the effect of dividing our result by 10, so instead of 16, we get 1.6 (near the 2" mark).

(Because we made an approximation when we wrote 2 at the 3" mark, the more we multiply or divide by 2, the more error we introduce.)

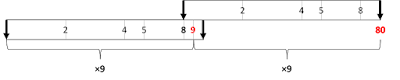
Based only on the fact that 2¹⁰ ≈ 10³, we are able to perform calculations involving multiples of 2 and 5. To write any more numbers on our ruler, we'll need to find other such coincidences. The insight we'll use next is that 8 × 10 ≈ 9 × 9.

If we line up our rulers to find 8 × 10, we find that the number 80 belongs at the 19" mark. Since 9 × 9 should also reach near the 19" mark, we should write 9 at the halfway point, near the 9½" mark.

(A better approximation would be to write the 9 at 9.54", which is closer to the 9 9/16" mark on a ruler.)

We got from 81 to its square root, 9, by cutting that length in half. We can cut that length in half again to find that 3 (the square root of 9) belongs near the 4¾" mark.

Multiply 2 × 3 to find 6. The correct value of 6 is around 0.778, nearest to the 7 13/16" mark.

To locate 7, we can use the fact that 5 × 10 ≈ 7 × 7.

We've now succeeded in making a simple slide rule, and along the way, we've learned how to use one to multiply or divide simple numbers. If we place 0.1, 0.2, ..., 0.99 on our slide rule (perhaps just as tick marks between integer values), then we could perform calculations with 2 significant digits.


Part 3:  Logarithms

Instead of using inches, let's label all positions on the ruler from 0.000 at the left edge to 1.000 at the right edge. In that case, we would write 3 near position 0.477 (what we previously referred to as the 4.77" mark of a 10" ruler). There is a simple relationship between these two numbers: 10^0.477 ≈ 3. In the language of logarithms, the notation "log 3" means "10 to what power is 3?" Therefore, we write log 3 ≈ 0.477. Here's a table of logarithms for the numbers we investigated earlier. (Technically, these are approximations of base-10 logarithms.)

 x     log x
 1     0.000
 2     0.301
 3     0.477
 4     0.602
 5     0.699
 6     0.778
 7     0.845
 8     0.903
 9     0.954
10     1.000

When we used our slide rule to compute 2 × 3 = 6, we were taking advantage of the fact that log 2 + log 3 = log 6. But why does that work?

First, some basics of logarithms. We know that 10³ = 1000, and therefore log 1000 = 3.

In 10³ = 1000, replace the 3 with the equivalent log 1000 to get:  10^{log 1000} = 1000.

Or, more generally: 10^{log A} = A

Using that and the fact that 10^A + B = 10^A × 10^B, we can work out log 2 + log 3 as follows:

10^{log 2 + log 3}
= 10^log 2 × 10^log 3
= 2 × 3
= 6

Since 10^{log 2 + log 3} = 6, then the definition of logarithms gives us log 2 + log 3 = log 6.

In general, log(A) + log(B) = log(A × B).

This fact lets us use our knowledge of just a few logarithms to compute many others. For example, since 98 = 2 × 7 × 7, we can find log 98 by calculating log 2 + log 7 + log 7 ≈ 0.301 + 0.845 + 0.845 = 1.991. Thus, we can factor any integer N into its primes and compute log N by adding up the logarithms of those prime factors.

Dave Computes Orbits and Projectile Motion

Part 1:  It's not a parabola.

When I'm standing on Earth and I throw a projectile in any direction and at any speed (less than escape velocity), most knowledgeable calculus or physics students will say that the projectile moves in a parabolic path. But that assumes that there is a constant downward acceleration.

What kind of path does the projectile follow when we take into account that the acceleration at its highest point is slightly less than the acceleration at the surface of the earth, and that the direction of that acceleration is always toward the center of the earth? The answer is surprisingly simple and illuminating.

Picture a satellite (of negligible mass) in orbit around the earth, moving in an elongated elliptical orbit:

(All diagrams in this post are the results of computer simulations.) We know that the satellite's acceleration depends only on the mass of the Earth and the distance to Earth's center. Thus, increasing the size of the Earth without changing its mass would have no effect on the satellite's orbit:

Things change only if the Earth grows so large that its surface intersects with the satellite's path:

Now, of course, the "satellite" crashes. When the Earth obscures enough of the elliptical path, the object is now more properly called a projectile, and the path appears to be parabolic:

So there's our answer. Projectiles, like satellites, follow elliptical paths. Always. Let's take that in for a moment. It means every time we throw a ball, we're really launching it into orbit around the center of the Earth--until the ground or other obstacle interrupts that orbit. Even a jumping human is briefly in orbit.


Part 2:  But it could be a parabola.

Imagine that an object above Earth's surface is given a horizontal velocity and then allowed to orbit the Earth in an elliptical path, as shown below. (The object's initial position is shown at the top of the orbit in each diagram.) Recall that an ellipse has two foci points. One focus is at the center of the Earth. If the initial velocity is relatively small, then the other focus is high above Earth's surface, just below the object's starting position.

If the object is given a larger initial velocity (still entirely in the horizontal direction), then the elliptical orbit grows wider and the second focus point moves closer to the Earth.

With a large enough initial velocity, the two foci meet in the center of the Earth, and a circular orbit occurs:

With an even larger initial velocity, the second foci moves to the other side of the Earth:

A larger initial velocity moves the focus further down in the diagram, and the orbit becomes longer and more eccentric.

With greater and greater initial velocities, the second focus moves as far down in the diagram as we wish, and the object moves as far away from Earth as we like, only to return again along its elliptical orbit.

At a certain high but finite velocity, the second focus point moves infinitely far away, and the object's path is no longer elliptical. Now the path is a parabola, and the object will escape Earth's gravity. Along this path, the object slows down more and more as it gets further and further from Earth, coming to a complete stop only at an imaginary point infinitely far away.

An even larger initial velocity now results in a hyperbolic path. Again, the object will never return, but now it will never slow down completely either. The second focus of the hyperbola now appears above the starting position, as if it wrapped around from infinity.

Neglecting relativistic effects (as I have throughout this post), in the limit, an arbitrarily large initial velocity will result in a horizontal path.

Part 3:  Further Thoughts

Barring velocities high enough to escape Earth's gravity, we've seen that an initially horizontal velocity always results in an elliptical path. But what about initial velocities with nonzero vertical components? No matter how its path starts, the object eventually reaches a point where its velocity is purely tangential, and that point will be the furthest or nearest point in an elliptical orbit aligned at some angle:

I used to think that an object needed to have just the right velocity to enter orbit, but now we see that a wide range of velocities result in elliptical orbits.

Not surprisingly, ellipses are the basis of orbital mechanics for spaceflight. For example, imagine a spaceship in a circular orbit around the Earth. Firing its rockets briefly to speed up puts it into an elliptical orbit that takes it further away from the Earth on its opposite side and then returns it to its starting point. If it briefly fires its rockets at its furthest point, it can enter a circular orbit at a larger radius.